2018年成人高考高起点文数考试章节难点解析（3）

难点3 运用向量法解题

平面向量是新教材改革增加的内容之一，近几年的全国使用新教材的高考试题逐渐加大了对这部分内容的考查力度，本节内容主要是帮助考生运用向量法来分析，解决一些相关问题.

●难点磁场

(★★★★★)三角形ABC中，A(5，-1)、B(-1，7)、C(1，2)，求：(1)BC边上的中线

AM的长;(2)∠CAB的平分线AD的长;(3)cosABC的值.

●案例探究

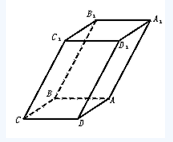
[例1]如图，已知平行六面体ABCD—A1B1C1D1的底面ABCD是菱形，且∠C1CB=∠C1CD=∠BCD.

成人高考高起点文数考试章节难点解析（3）chengkao1.png" style="margin: 0px; padding: 0px; border: 0px; text-align: left; vertical-align: top;"/>

(1)求证：C1C⊥BD.

(2)当 的值为多少时，能使A1C⊥平面C1BD?请给出证明.

命题意图：本题主要考查考生应用向量法解决向量垂直，夹角等问题以及对立体几何图形的解读能力.

知识依托：解答本题的闪光点是以向量来论证立体几何中的垂直问题，这就使几何问题代数化，使繁琐的论证变得简单.

错解分析：本题难点是考生理不清题目中的线面位置关系和数量关系的相互转化，再就是要清楚已知条件中提供的角与向量夹角的区别与联系.

技巧与方法：利用a⊥b a·b=0来证明两直线垂直，只要证明两直线对应的向量的数量积为零即可.

(1)证明：设 =a, =b, =c,依题意，|a|=|b|， 、 、 中两两所成夹角为θ，于是 =a-b， =c(a-b)=c·a-c·b=|c|·|a|cosθ-|c|·|b|cosθ=0,∴C1C⊥BD.

(2)解：若使A1C⊥平面C1BD，只须证A1C⊥BD，A1C⊥DC1，

由 =(a+b+c)·(a-c)=|a|2+a·b-b·c-|c|2=|a|2-|c|2+|b|·|a|cosθ-|b|·|c|·cosθ=0,得

当|a|=|c|时，A1C⊥DC1，同理可证当|a|=|c|时，A1C⊥BD，

∴ =1时，A1C⊥平面C1BD.

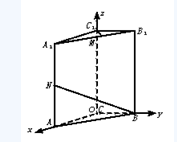
[例2]如图，直三棱柱ABC—A1B1C1，底面△ABC中，CA=CB=1，∠BCA=90°，AA1=2，M、N分别是A1B1、A1A的中点.

(1)求 的长;

(2)求cos< >的值;

(3)求证：A1B⊥C1M.

命题意图：本题主要考查考生运用向量法中的坐标运算的方法来解决立体几何问题.属

★★★★级题目.

知识依托：解答本题的闪光点是建立恰当的空间直角坐标系O-xyz,进而找到点的坐标和求出向量的坐标.

错解分析：本题的难点是建系后，考生不能正确找到点的坐标.

技巧与方法：可以先找到底面坐标面xOy内的A、B、C点坐标，然后利用向量的模及方向来找出其他的点的坐标.

(1)解：如图，以C为原点建立空间直角坐标系O-xyz.

依题意得：B(0，1，0)，N(1，0，1)

∴| |= .

(2)解：依题意得：A1(1，0，2)，C(0，0，0)，B1(0，1，2).

∴ = =(0，1，2)

=1×0+(-1)×1+2×2=3

| |= (3)证明：依题意得：C1(0，0，2)，M( )

∴ ∴A1B⊥C1M.

●锦囊妙计

1.解决关于向量问题时，一要善于运用向量的平移、伸缩、合成、分解等变换，正确地进行向量的各种运算，加深对向量的本质的认识.二是向量的坐标运算体现了数与形互相转化和密切结合的思想.

2.向量的数量积常用于有关向量相等，两向量垂直、射影、夹角等问题中.常用向量的直角坐标运算来证明向量的垂直和平行问题;利用向量的夹角公式和距离公式求解空间两条直线的夹角和两点间距离的问题.

3.用空间向量解决立体几何问题一般可按以下过程进行思考：

(1)要解决的问题可用什么向量知识来解决?需要用到哪些向量?

(2)所需要的向量是否已知?若未知，是否可用已知条件转化成的向量直接表示?

(3)所需要的向量若不能直接用已知条件转化成的向量表示，则它们分别最易用哪个未知向量表示?这些未知向量与由已知条件转化的向量有何关系?

(4)怎样对已经表示出来的所需向量进行运算，才能得到需要的结论?